One of the key hurdles to building a large quantum computer is maintaining the coherence of the many individual two-level quantum mechanical systems, or qubits. Atoms and ions in a vacuum or nuclear spins in solids and liquids can have long coherence, but it is not yet known how well those systems can be scaled to make a large computer. Ideally one could use the spin of an electron in a semiconductor as a qubit, since modern semiconductor technology is based upon moving and controlling electrons in silicon. However, the coherence time for electron spins in semiconductors is typically nanoseconds or microseconds, with the longest measured times being a few tens of milliseconds in silicon. Princeton researchers, in collaboration with a group at Oxford (initiated under the Oxford-Princeton Research Partnership) and at Lawrence Berkeley National Lab have shown that they can transfer a quantum state from an electron bound to a phosphorus donor atom in silicon, to the phosphorus nucleus, and then back to the electron. While stored in the nucleus, the quantum state stays coherent for over 1 second. This results brings us a step closer to a solid state quantum computer.
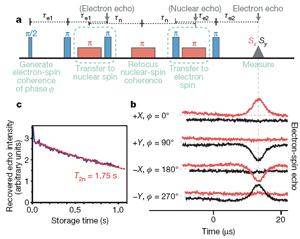 Coherent storage of an electron-spin state in a nuclear-spin state, using a 31P-doped 28Si-enriched silicon single crystal. a, The general sequence for the storage and retrieval of the electron-spin state comprises microwave and RF pulses applied at certain times, defined by te1, te2 and tn. b, An electron-spin coherence is stored in the nuclear spin for 2tn≈50 ms, at 7.2 K. Real (red) and imaginary (black) parts of the recovered electron-spin echo are shown for different initial phases, àŽ’¦. The echo is of comparable intensity to that obtained at the beginning of the sequence, even though the electron-spin coherence time, T2e, is about 5ms here. The lifetime of the stored state is limited instead by the nuclear decoherence time, T2n, which can be measured directly by varying tn. c, The recovered echo intensity was measured as a function of the storage time at 5.5 K while a dynamic (Carr-Purcell-Meiboom-Gill) decoupling sequence was applied to the nuclear spin, yielding a T2n exceeding 1 s.
Coherent storage of an electron-spin state in a nuclear-spin state, using a 31P-doped 28Si-enriched silicon single crystal. a, The general sequence for the storage and retrieval of the electron-spin state comprises microwave and RF pulses applied at certain times, defined by te1, te2 and tn. b, An electron-spin coherence is stored in the nuclear spin for 2tn≈50 ms, at 7.2 K. Real (red) and imaginary (black) parts of the recovered electron-spin echo are shown for different initial phases, àŽ’¦. The echo is of comparable intensity to that obtained at the beginning of the sequence, even though the electron-spin coherence time, T2e, is about 5ms here. The lifetime of the stored state is limited instead by the nuclear decoherence time, T2n, which can be measured directly by varying tn. c, The recovered echo intensity was measured as a function of the storage time at 5.5 K while a dynamic (Carr-Purcell-Meiboom-Gill) decoupling sequence was applied to the nuclear spin, yielding a T2n exceeding 1 s.