In solids, the kinetic energy of an
electron generally increases as the square of its momentum. By contrast, in a
Topological Insulator such as Bi2Te2Se, electrons on the surface are
predicted to be Dirac Fermions for which the energy increases linearly with
momentum. In a magnetic field B, the
allowed states of an electron are quantized into Landau Levels (LLs). The
sequential emptying of occupied LLs in an increasing field leads to quantum
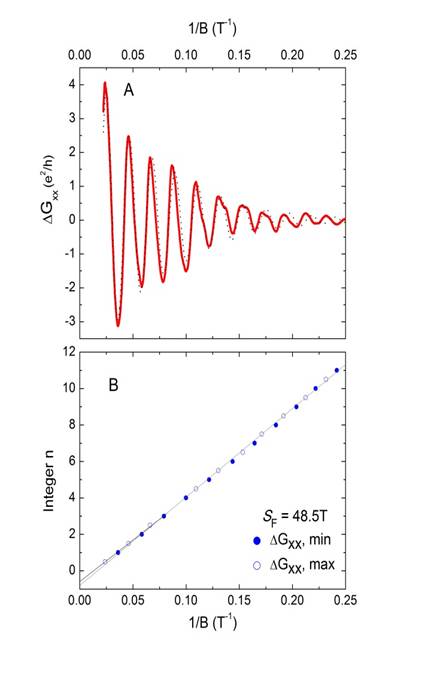
oscillations in the conductance Gxx (Fig. 1A). A key signature of Dirac
Fermions is the existence of an extra half-period in the oscillations called “π-Berry
Phase shift”. (Technically, this arises from the ½ Landau Level that exists at
zero energy.) The quantum oscillations provide an elegant way to “count”
directly the available levels. By plotting the fields Bn of the minima in Gxx against the integer n (n
counts the number of levels still to be emptied), one may determine the
ultimate value of n by extrapolation to infinite field (1/Bà 0).
Measurements to 45 Teslas on a
crystal of Bi2Te2Se by Xiong et
al.
[1] reveal that there is ½ level left (Fig. 1B), consistent with Dirac
Fermions. The uncertainties in this experiment are unusually low because of the
large number of oscillations observed and the low index of the last datum (n = ½).
The results provide firm evidence that the oscillations in Bi2Te2Se
indeed arise from Dirac Fermions.